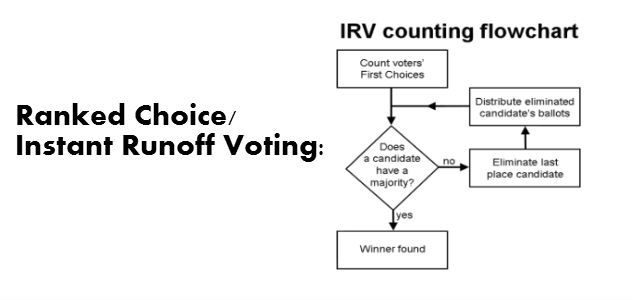
Ranked choice voting advocate says that election method reforms are underappreciated cure all
Democracy, elections and voting at Democracy Chronicles
A Plan to Improve the American Electoral System (via Socialpost)
Van Cornelius Activist Post
Once again this past election I could not find a candidate that I could whole-heartedly support. If I voted for a non-major party candidate (in my case, the Libertarian Party candidate), I ran the risk of contributing to the election of my least-favored major-party candidate.

Michael Ossipoff says
It’s good to hear advocacy of better voting systems. The rank-count that you described, as an alternative to Instant Runoff, is called the Bucklin system. It was used in some municipal elections for a while, during the first decades of the 20th century.
Nowadays, when people propose or speak of Bucklin, they refer to ER-Bucklin. That’s Bucklin, but with the option to rank as many candidates as you want to, at any rank position. The “ER” stands for “equal ranking”.
The better form of ER-Bucklin, and the one that is actually sometimes advocated and discussed, is the version in which, when your ballot gives to the next lower rank position, it gives a whole vote to each candidate whom you’ve ranked at that rank position.
ER-Bucklin, in the above-described form, is considerably better than Instant Runoff, because ER-Bucklin meets the FAvorite-Betrayal Criteion. No one has any strategic incentive or need to vote anyone over their favorite. When people strategically need to bury their favorite, that makes nonsense out of the election result.
As defined at the electowiki, ER-Bucklin has another feature:
When your votes arrive at a certain rank position, in which you have N candidates, your ballot delays for N-1 rounds before it gives votes to its _next_ lower rank position.
Here’s the reason for that delay:
Say there’s a majority who prefer X and Y to everyone else, and rank X and Y over everyone else. If equal ranking isn’t allowed, and you’ve only ranked one candidate in each rank position, then, as votes are given to next rank positions, during the rounds, eventually that majority will have given a majority vote-total to either X or Y.
How could they not? Every member of that majority ranks both X and Y over everyone else, and so, eventually, before giving to anyone else, they’ll have concentrated a majority vote total on X, Y, or both.
But now, what if equal ranking is allowed? If you’ve ranked lots of candidates at a rank position, then you’ll next give to your next lower-ranked candidates much sooner than you would have if you’d ranked sequentially. That means that, though you’ve ranked X and Y over everyone, you can give your votes _prematurely_ to lower-ranked candidates, before the rest of that {X<Y} majority have given X or Y a majority.
Without the equal ranking, Bucklin meets the Mutual Majority Criterion, which says:
If a majority of the voters prefer the candidates in set S to all of the other candidates, and vote sincerely, then the winner should come from S.
[end of Mutual Majority Criterion definition]
But, if the delay that I spoke of earlier is added to ER-Bucklin, then your ballot won't give votes to its next lower rank position any sooner than it would have if the equal ranked candidates had been ranked sequentially on your ballot.
So, with that delay, ER-Bucklin meets the Mutual Majority Criterion.
Regrettably, Bucklin and ER-Bucklin don't get rid of the chicken dilemma. I claim that there's no excuse for a rank method to not get rid of the chicken dilemma.
Though the chicken dilemma isn't a problem for Approval and Score, it is a nuisance to deal with.
When there are unacceptable candidates who might win, even for the best rank methods, the best that they can do, strategially, is to have the same optimal strategy as Approval or Score. But there is one way that some rank methods can improve on Approval and Score: Some rank methods can get rid of the chicken dilemma. In my articles here, I've described two such rank methods: ICT and Symmetrical ICT. Their definitions can be found in the recent article entitled "Properties, Part 3: Improved Condorcet". Also, Symmetrical ICT is defined at the electowiki (search for it in google).
Anyway, because getting rid of the chicken dilemma is the only way that rank methods can genuinely improve on Approval and Score in u/a elections (elections in which there are unacceptable candidates who could win), and because there are rank methods that can get rid of the chicken dilemma, then there's no reason to propose or use a rank method that doesn't get rid of the chicken dilemma.
That's why I don't propose Bucklin or ER-Bucklin, or mention it in my articles.
Here's what I meant when I said that rank methods don't improve on Approval's strategy.
In a u/a election, Approval's optimal strategy is to approve all of the acceptable candidates and none of the unacceptable candidates.
Score's optimal strategy is to top-rate the acceptables and bottom-rate the unacceptables.
ER-Bucklin's optimal strategy is to top-rank all of the acceptables, and not rank any unacceptables.
As I said, the best that any rank method can do, in a u/a election, is to duplicate Approval's optimal strategy.
…unless a method, such as ICT or Symmetrical ICT, can get rid of the chicken dilemma.
Bucklin and ER-Bucklin don't get rid of the chicken dilemma. So they don't qualify as proposals.
Approval and Score are my recommendations for our official public elections.
As for IRV, its failure of FBC disqualifies it from consideration for official public elections, with our current electorate.
The Greens' platform proposes IRV. As I said in one of my articles, any electorate that could elect the Greens, using Plurality, would be compettent to make good use of IRV. So IRV would be ok then. But, with the electorate that we have now, IRV is completely inadequate, due to its FBC-failure.
Michael Ossipoff